Skip to content

Secondary ports and Computation of rates

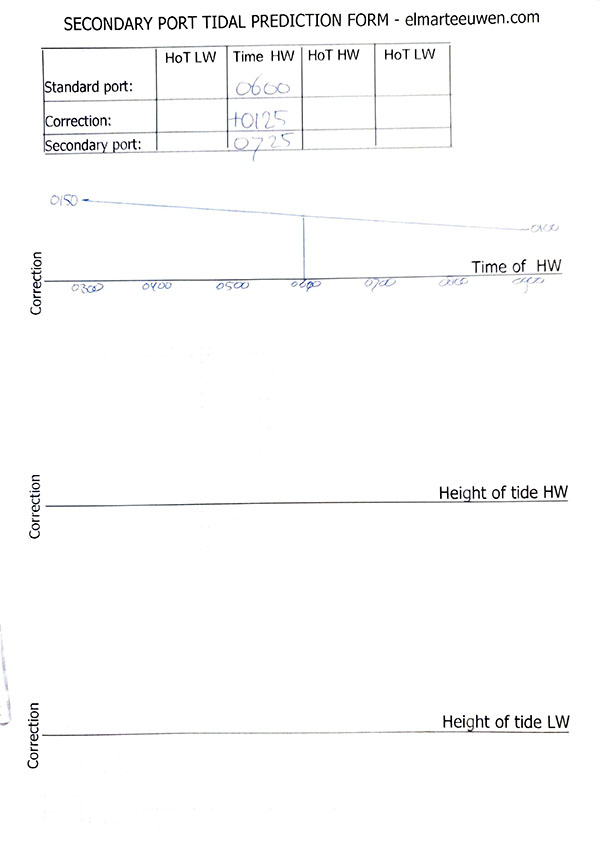
Secondary port tidal prediction form

If a particular port is a secondary port and we want to calculate the rise at a particular time, we need to use the tidal graph of the standard port. To use that graph we always need 3 pieces of data:

The time of high water (Time of HW)
Height of Tide High Water (HoT HW).
Height of Tide Low Water (HoT LW).

With those 3 data, we can fill in and apply the graph for exact interpolation (see revious article). Now we have to calculate that data by adding the (sometimes negative) correction in the secondary port. We find the correction by interpolating. For this purpose, I developed the Secondary port tidal prediction form.

secondary-ports-tidal-prediction-formDownload
exact interpolation method

different time zones and DST

The first thing I recommend doing is making a table with the times, because sometimes the onboard time is different from a different Time Zone than the local time requested. Moreover, sometimes Daylight Saving Time DST applies. So I recommend converting all times to Standard Time in the Standard Port first. This is not always UT, but can also be TZ-01.00. If the answer has to be given in a different time, e.g. DST, calculate that at the last moment at the end of the sum.

After all the times you write down, write what time it is.

For example: 13.00 TZ -0100 DST or, say, 17.00 UT.
TZ 0000TZ -0100
UTUT +1
12.00 standard time (= 13.00 DST)13.00 standard time (=14.00 DST)

Calculate time of high or low water in a secondary port

  1. Find the time of HW or LW of the Standard port (you can tell by the arrow whether to browse forward or back to find the standard port). This means browse to Standard Port – > and this means browse back to Standard Port <-
  2. Determine the time difference using the times/differences table.
  3. Add the time difference to the time in Standard Port.
    For example: In the Reeds NA, at the Secondary Port Scheveningen (Primary Port is Vlissingen) you will find this table:
    Times
    High Water Low Water
    0300 0900 0400 1000
    1500 2100 1600 2200
    Differences SCHEVENINGEN
    +0150 +0100 +0220 +0245
  • If the time of high water in Standard Port Vlissingen occurs at 03:00 or 15:00, then it is high water in Scheveningen 01:50 later. So at 04:50 and 16:50.
  • If the time of high water in standard port Vlissingen occurs at 09:00 or 21:00, then it is high water in Scheveningen 01:00 hours later. 10:00 so, or 22:00.
  • If the time of high water in the Standard Port Vlissingen occurs at 06:00 or at 18:00, then it is 01:25 later high water in Scheveningen, as 06:00 lies between 03:00 and 09:00 and so interpolation must be made between 01:50 and 01:00.

This interpolation is sometimes tricky and is best done with my secondary port tidal prediction form with the timeline on the x-axis and the correction time on the y-axis. Note that the correction time can also be negative, in which case you put the correction times on the negative y-axis. Keep in mind that this is actually very similar to linear interpolation as 1/7 rule is used to calculate rise between spring and neap tides. So in this case, we are actually talking about a kind of 1/6 rule, because there are always 6 hours between the values we use.

secondary port tidal prediction form 1

If you have filled in the my secondary port tidal prediction form neatly then you can read the value without calculating. Also, the form makes it easier for you to write down the formula to calculate the correction exactly.

In the above case, there is:
on the x-axis between 0300 and 0900, 6 hours of 60 minutes is thus 360 minutes.
on the y-axis between 0150 and 0100, 50 minutes difference.

0150 – (0050/360 x 180) = 01.25

Always check that your calculated answer matches the value you had read off in the form.

Calculate Height of tide at high or low water in a secondary port

  1. Look for the rise in Standard Port.
  2. Determine the difference in the Secondary Port using the table below found at the Secondary Port in the Reeds Almanac.

    Heights (metres )
    MHWS MHWN MHLN MLWS
    4.7 3.8 0.8 0.2
    – 2.6 -2.1 -0.6 0.0
  3. Rise in the Secondary Port = Rise in the Standard Port + correction:
    a. If the rise in the Standard Port at high water is 4.7 metres, then the rise in the Secondary Port is 2.6 metres lower, i.e. 2.1.
    b. If the rise in the Standard Port at high water is 3.8 metres, then the rise in the Secondary Port is 2.1 metres lower, i.e. 1.7.
    c. If the rise is between 4.7 and 3.8, interpolate (or if it is outside it, say 4.9, extrapolate). To do this, again draw a graph similar to the previous example, with the x-axis showing the rise and the y-axis showing the correction.

    For example: HW in the standard port is 4m and the subsequent LW in the standard port is 0.6m.
    What will be the values in the secondary port?
    The answer and elaboration is given below.
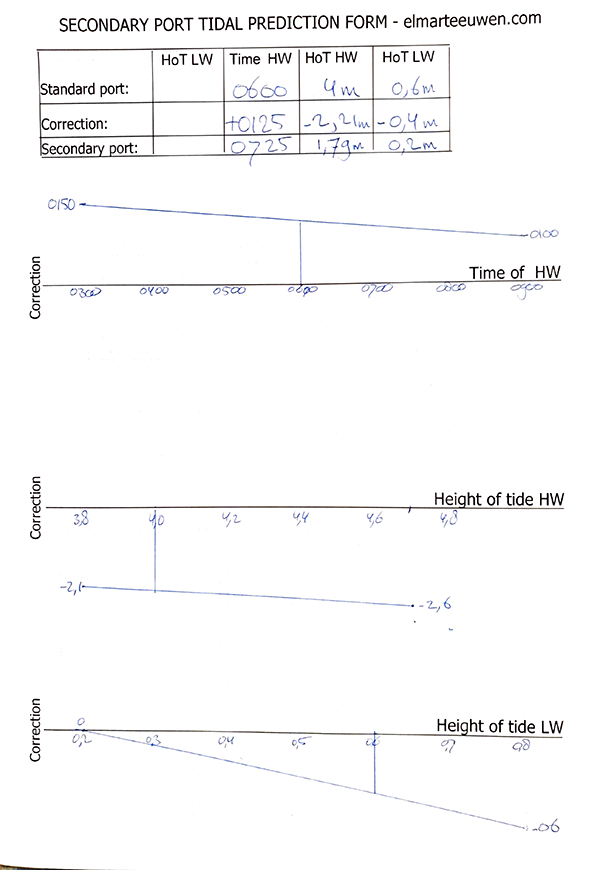
secondary port tidal prediction form 2

We can read or calculate the corrections:

Correction HoT HW:
Difference on the x-axis is 4.7 – 3.8 = 0.9m
Difference on the y-axis is 2.6 – 2.1 = 0.5m
-2.1 – (0.2 x 0.5/0.9) = – 2.21 correction

Correction HoT LW:
Difference on the x-axis: 0.8 – 0.2 = 0.6m
Difference on the y-axis: 0.6m
0 – (0.4 x 0.6/0.6) = – 0.4m

Secondary Port

We want to use the exact interpolation method to determine what the rise at 10.50 is. The tide table of the corresponding Standard port states the following:

Time m
08.30 4,1
15.01 1,0

The secondary port states the following:

 Times   Heights(metres) 
HighWaterLowWaterMHWSMHWNMLWNMLWS
01000700010007004,83,91,40,5
1300190013001900    
Differ.       
-0105-0005-0035-0035+0,4+0,2+0,2+0,2

Of course, we solve this by applying the graphical exact interpolation method, as already explained in the Coastal Navigation course. But in order to plot the tidal graph, we must first calculate the rise and time of HW and LW in the secondary port, by applying the corrections to the standard port data, and for this we use the secondary ports tidal prediction form.

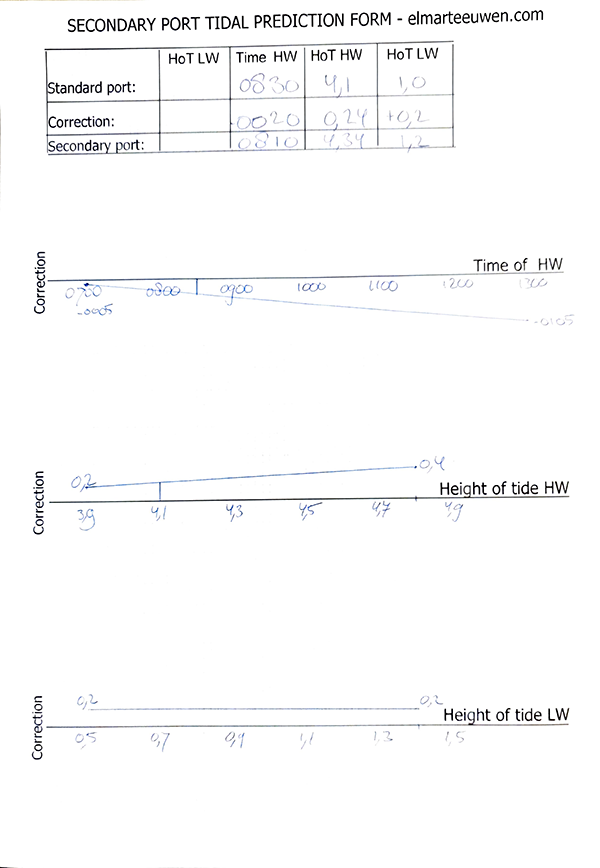
secondary port tidal prediction form 3

Correction HW Time: 0005 – (1.5 hours / 6 hours) x 60 min = – 0020
Correction HW Heights 0.2 +( 2/9 x 0.2) = + 0.24
Correction LW Heights = + 0,2

Computation of rates

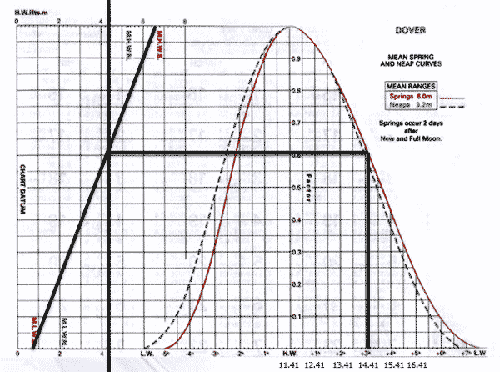
This method assumes that the current rate varies with the range in Dover. This in itself is logical, because if the range in Dover is large then there will also be a strong current. Moreover, if the range in Dover is large then the range in the rest of Europe will also be large. The computation of rates is a more accurate way than interpolating with the average current rate at spring tide and neap tide that you see in the table in the chart or the HP33. There you see 1020 and that means 2.0 knots at spring tide and 1.0 knot of current at neap tide.

  1. Note the Time of HW in the Standard Port.
  2. Calculate the range in metres. This is needed to determine whether it is spring tide, neap tide or in between. Later, we will plot these on the vertical axis.
  3. Note time of Departure (ETD) and Arrival (ETA).
  4. After each time, write what time it is.
    E.g. BT = TZ -0100 DST. That then stands for on-board time and that is Time Zone -0100 Daylight Saving Time.
  5. Determine how many hours before or after HW you leave and arrive by drawing a timeline.

    For example a:
    HW in the standard port is 14.25 UT
    ETD 11.55 UT
    ETA 12.25 UT
    -3 -2 -1 HW
    __|_____|____|______|______|_____|______|
    11.25 12.25 13.25 14.25
    So we sail for 30 minutes in this case and we can look up the current in the current-diamond table at HW-2, because the ETD 11.55 is exactly between HW-3 and HW-2 and we end the voyage exactly at HW-2.

    Example b:
    HW in the standard port is 14.25 UT
    ETD 12.25 UT
    ETA 13.25 UT
    -3 -2 -1 HW
    __|_____|_____|_____|______|_____|______|
    11.25 12.25 13.25 14.25
    In this case, we sail for 1 hour, with the first half-hour in HW-2 and the second half-hour in HW-1. So we have to look up the current rate 2 times and determine the average direction and speed.
  6. Draw a vertical line from the current velocity at spring tide to the red horizontal Spring tide line.
  7. Draw a vertical line from the current velocity at neap tide to the blue horizontal neap tide line.
  8. Draw a diagonal line between the intersections of the vertical lines with the horizontal lines of spring and neap tides.
  9. Draw a horizontal line from the average range in the standard port on the vertical axis to the diagonal line
  10. Draw a vertical line to read the current rate on one of the horizontal axes.
  11. Note. In the above example, the journey took only 30 minutes, so the flow rate found must then still be divided by 2.
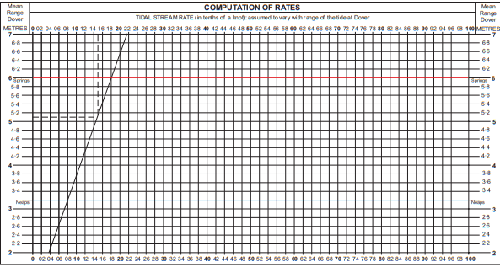
computation of rates

Note that the horizontal line of the day in question, is almost always below the red spring tide line and above the blue neap tide line, unless it is a situation of extreme spring tide or neap tide.

Variations in tides

The Moon’s orbit is periodically rounder and then more oval; it is never a perfect circle. The point where it is closest to Earth each month is called its periapsis (this varies throughout the year). The point where the moon is furthest from the earth each month is called apogee (this also varies throughout the year). Full moon near periapsis is a “supermoon”

Each area also varies whether high tides occur once or twice:
Daily tides: 1 high 1 low per 24 hours
Semi-daily: 2 times high and 2 times low (both more or less equally high) per 24 hours
Mixed semi-daily or mixed tides: One high high water and one lower high water per 24 hours.

Calculating solar and lunar rises and sets

Of course, it is important to know what time the sun and moon set and rise, so that we can take this into account when planning the trip. For this purpose, tables are available that show this for a given position each day.

Do realise that the timing of the phenomenon varies for each position. So those tables are not accurate to the minute for every position. Normally, a few minutes makes little difference, but if we want to navigate with the sextant, we need to know at the minute what time to shoot the stars. This is because this is only possible when the sun has just disappeared behind the horizon, so we can see both the horizon and the stars. If we were to check every time whether the sun has already set, we would be blinded and unable to shoot a star accurately with the sextant. Several nautical books contain tables with the times for the various phenomena for a given standard position. They also include tables with the correction factors for longitude and latitude other than that standard position.

What it broadly boils down to is the following: If you are west of the standard position, for example, the sun will rise later and set later. If you are north of the standard position, then in summer the sun will rise earlier and set later. In winter, the sun there would rise later and set earlier. (This applies to the northern hemisphere).

You can add 4 minutes for every degree west of the standard position or subtract 4 minutes for a position east of the standard. After all, the earth is 360 degrees round and rotates around its axis in 24 hours. 360 degrees x 4 minutes is 1440 minutes. 1440/60 = 24 hours.

4 minutes per longitude equals 1 minute (time) per 15 minutes (length).

Questions & Answers

Please print these data before you begin with the questions below.

Question 1: In the tide table in the Almanac you can see that the height of tide at high tide is 2.4m, and at low tide 0.5m. What is the depth at HW in places where the chart depth is 0.6 meters? (Note: 0.6 is underlined “depth”)

a: 3.00
b: 1,60
c: 1,80

Question 2: In the map we find 1.5m (underlined, so above CD). The height of tide at HW is 3.2 meters; at LW 1.2 meters. How much water can at LW be expected at this location?

a: 1 meter
b: 0.5 meters
c 1.5 meters

Question 3: The Height of tide at a certain place at high tide at spring is 5 meters. The height of tide at high tide neap is 2.9 meters. What will be the height of tide at HW 3 days after spring tide?

a: 2.9 meters
b: 3.9 meters
c: 4.1 meters

Question 4: Data for Vlissingen: HW 04.55 4.9 m LW 11.18 0.5 m Calculate the height of tide at 06.55

a: 4.0 meters
b: 3.8 meters
c: 3.3 meters

Question 5: Height of tide at high-water is 4 meters and at low water 1.6 meters. The time between HW and LW is 6 hours. How much water above the chart datum can be expected 2 hours after HW?

a: 3.4 meters
b: 2.4 meters
c: 2.0 meters

Question 6: What is the height of tide in Westkapelle 4 days after full moon (=2 days after spring) 2 hours before high tide? (Calculate with the 1/7 rule and the 1/12 rule.) In the chart the square table says: MHWS 4.2, MHWN 3.4, MLWN 0.8, MLWS 0.3

a: 3.9 meters
b: 4.1 meters
c: 3.1 meters

Question 7: According to your GPS, you sail at 11.00 am on a 10 meter depth line (= chart depth). At 08.00 it was low tide (0.4m) and at 14.00 it is high tide there (4.7m). The time between HW and LW is 6 hours. What is the water level at the ten-meter depth line at 11.00?

a: 11.10 meters
b: 12.55 meters
c: 13.20 meters

Question 8: Use the PDF with data for this. What is the rise on December 10 at 09:00 in Vlissingen?

a: 17 DM
b: 31 DM
c: 8 DM

Question 9: To be able to sail over a sill near Vlissingen, you need at least 2.5 meters height of tide. What time can you cross that sill on December 9th?

a: from 07.00 to 16.00
b: from 13.00 to 16.00
c: from 07.00 to 13.00

Question 10: What is the exact time of low tide in the afternoon on December 21 in Vlissingen?

a: 14.14
b: 01.36
c: 20.40

Question 11: What is the height of tide on December 9, 2007 at 11 a.m. in Vlissingen? In the Reeds the tide table for December 9, 2007 states: At 07.56 0.7m. And at 13.49 4.5m. Moreover, it is 2 days before spring tide. (All times are in UT+1).

a: 2.1 meters
b: 1.8 meters
c: 1.6 meters

Question 12: To be able to sail over a shoal near Vlissingen, you need at least 2.5 meters of rise. What time can you cross that shoal on December 9? In the Reeds the tide table for December 9, 2007 states: At 07.56 the rise is 0.7m. And at 13.49 the rise is 4.5m. Moreover, it is 2 days before spring tide. (All times are in UT+1).

a: From 10.26 to 17.30
b: From 11.26 to 16.10
c: From 11.26 to 17.10

Question 13: What is the height of tide west of the Roompot lock on June 14, 2007 at 6:00 PM local time?

The tidal data of the standard port Vlissingen are (times in UT+1):

13:08 4.6
19:35 0.3

We also see that it is 2 days before spring tide.

The table with differences in Time and HOT (Height of Tide) between the Standard Port and Secondary Port states:

Time HW

  0900 1500
+0005 -0015

HOT HW
3.8 4.8
-0.8 -1.2

HOT LW
0.2 0.8
+0.1 -0.2

a: 1.3 meters.
b: 1.7 meters
c: 2.1 meters

Question 14: A ship comes from sea and is considering sailing onto the Oosterschelde and going to Roompot Marina. In what time frame can we pass under the fixed bridge of the Roompot lock on June 1, 2007? The mast is 17.30 and you want to maintain a 50cm safety margin. Suppose the fixed bridge is 17 meters high above Mean Sea Level (MSL) and that MSL is 2 meters above the chart datum. In what time period could you sail under the bridge?

The table of the standard port Vlissingen states:

08.19 0.4m
14.19 4.5m

Moreover, we see that it is 1 day before spring tide.

The table with differences in Time and HOT (Height of Tide) between the Standard Port and Secondary Port states:

Time of HW
  0900 1500
+0005 -0015

HOT HW
  3.8 4.7
-0.9 -1.1

  HOT LW
  0.2 0.8
+0.1 -0.2

a: Until 10.47 or after 18.17
b: Until 11.47 or after 19.17
c: Until 12.47 or after 4.17

Question 15: What is the direction of the tidal current off the coast of Vlissingen when it is HW Hoek van Holland and spring tide?

a: northeast; 1.5 kn.
b: northeast; 0.8 kn.
c: southwest; 1.5 kn.

Question 16: Using the diagram of the Computation of rates, calculate the current rate at 140:00 if the current shown in the chart is: 4022, or: 4.0 knots at spring tide and 2.2 at neap tide.

11.00 6.1
17:00 1.2
23:00 6.3
05.00 1.3

a: 3.0
b: 2.3
c: 3.3 kn

Question 17: What is the tidal current if it is 4 hours after HW Dover at Calais at neap tide?

a: 0.6 Kts, towards the north-east
b: 1.2 Kts, heading south west
c: slack

Question 18: Does the sun rise earlier or later in Brittany in winter than it does here in Zeeland?

a: same
b: later
c: earlier

Question 19: Will it get dark earlier or later in Brittany on June 1 than in Zeeland?

a: later
b: earlier
c: same

Question 20: If the sun were to rise at 06.15 UTC at 4º east longitude. What time does the sun rise, at 0º 15′ west longitude?

a: 05.55
b: 06.00
c: 06.32

Answers
Course overview